통계 기초 : the meaning of power (통계 파워의 의미) + 알파 + 베타 기본 콘텐츠로 건너뛰기

통계 기초 : the meaning of power (통계 파워의 의미) + 알파 + 베타

 통계를 처음 공부할 때, 마주하는 아주 중요한 개념들이 있다. 

특히 통계적인 검정을 하고자 할 때, 기초적 검정이든 고급 검정이든 이번에 정리하고자 하는 개념들은 항상 사용되기 때문에 확실하게 알고 가는 것이 좋다. (항상 헷갈림)


📙 1. 통계학개론과 같은 교재에서 '검정(hypothesis test)' 파트에 도달하면 가장 먼저 나오는 단어(?) 중에 하나가 '알파α'이다.

통계에서 알파α는 유의 수준(significance level)이라는 개념을 갖고 있다.

유의 수준은 제 1종의 오류(=귀무가설이 사실인데 기각하는 오류)를 허용할 확률이다. 유의 수준으로는 5%가 많이 사용되는데, 이는 제 1종의 오류를 허용할 확률이 5%라는 의미이다. 따라서 통계 검정시 유의 확률(p-value)이 유의 수준(significance level)인 5%보다 작으면 귀무가설을 기각하게 되는 것이다.

알파를 간단하게 정리하면 다음과 같이 나타낼 수 있다.

📌 알파 = 유의 수준 = 제 1종의 오류 = 위양성

α (alpha) = significance level = type 1 error = false positive


📘 2. 검정(hypothesis test) 파트에서 알파 다음으로 나오는 개념이 '베타β'이다.

 알파α가 제 1종의 오류를 나타냈다면, 베타β는 제 2종의 오류(=귀무가설이 거짓인데도 기각하지 않는 오류)를 나타낸다. 제 2종의 오류는 제 1종의 오류보다는 상대적으로 덜 치명적이긴 하지만, 여전히 오류라는 사실을 벗어날 수 없다.

베타를 간단하게 정리하면 다음과 같이 나타낼 수 있다.

📌 베타 = 제 2종의 오류 = 위음성

β (beta) = type 2 error = false negative


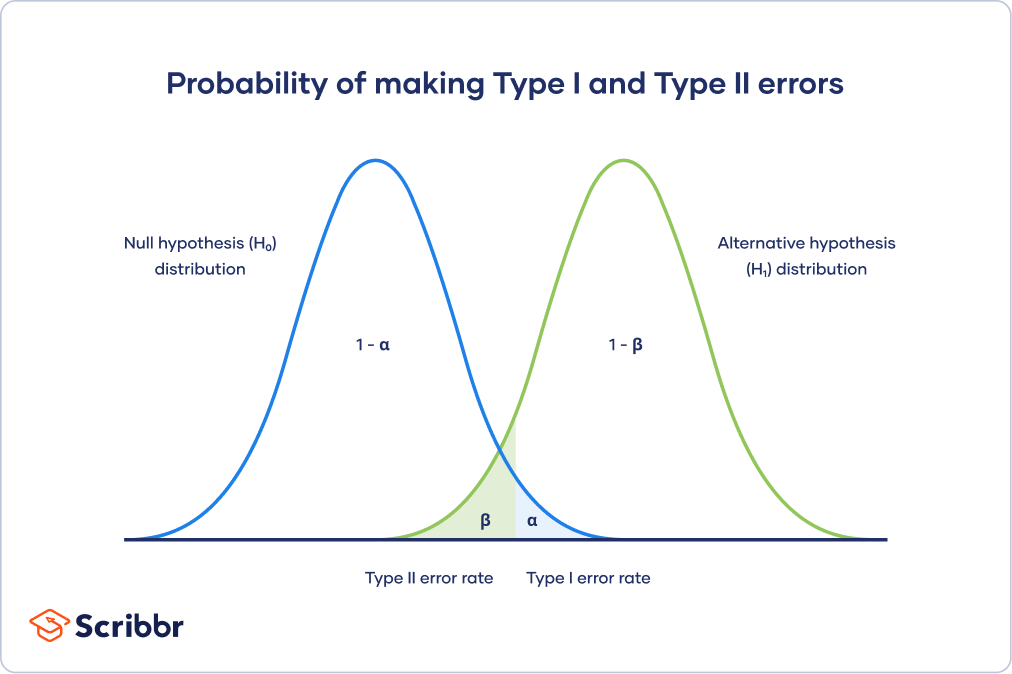
이를 그림으로 나타나면 다음과 같다. (출처는 scribbr)


📋통계에서 검정력(=Power)이라 불리는 개념은 1에서 베타를 뺀 것이다.

즉, '검정력=Power'는 1에서 제 2종의 오류 확률을  뺀 것으로, 귀무가설이 거짓일 때 귀무가설을 기각할 확률이며, 이는 대립가설이 참일 때 대립가설을 받아들일 확률로, True Positive일 확률이다.

 검정력을 간단하게 정리하면 다음과 같다.

📌 Power in statistics

    = 1 - β (beta)

    = 1 - type 2 error

    = 1 - Pr(False Negative)

    = True Positive

    = probability of accepting an alternative hypothesis when the alternative hypothesis is true.

    =Pr(reject H0 | H1 is true)

    = Sensitivity


따라서 높은 통계적 검정력이란 의미는 제 2종의 오류의 risk가 작다는 것을 의미한다.

"High statistical power" means there is small risk of having type 2 errors(false negative).


이론적으로는 제 2종의 오류와 제 1종의 오류를 모두 줄이는 것이 좋지만 불가능하다. 알파를 작게하면 베타가 커지고, 베타를 줄이면 알파가 커진다.

예를 들어, Bonferroni correction을 하게 되면 제 1종의 오류를 줄이게 되는, 매우 보수적인 방법이다. 따라서 Bonferroni correction을 적용하면 제 2종의 오류 확률이 증가하게 된다.

반대도 마찬가지이다. 제 2종의 오류를 줄이려 한다면 귀무가설을 기각할 확률이 증가하므로 제 1종의 오류가 증가하게 된다.


아래 표를 가지고도 생각해볼 수 있다.


Predicted
Positive Negative
Actual Positive True Positive (TP) False Negative (FN)
= beta
Negative False Positive (FP)
= alpha		 True Negative (TN)
라벨:

댓글

댓글 쓰기

이 블로그의 인기 게시물

통계 기초 : 확률 분포 - (1) 이항분포

Binomial distribution 이항분포에 앞서 베르누이분포가 있다. 모든 가능한 결과가 두 가지인 실험(표본공간이 {불량품, 양호품},{찬성, 반대} 등)을 베르누이 시행(Bernoulli trial)이라 한다. 성공확률을 p 라고 할 때, '성공'이면 1, '실패'면 0으로 대응시키는 확률변수를 베르누이 확률변수라 한다. 베르누이 확률변수 X의 확률분포는 다음과 같이 정의할 수 있다. $$ P(X=x) = p^{x}(1-p)^{1-x}, x=0,1 $$ 따라서, X=0인 경우에는 P(X=0) = (1-p)이고, X=1인 경우에는 P(X=1) = p가 된다. 베르누이분포의 평균은 E(X)=p, Var(X)=p(1-p) 이다. 이처럼 동일한 성공확률을 가진 베르누이 시행 을 독립적 으로 반복 하여 시행할 때, 'X=성공횟수'의 분포를 이항분포(binomial distribution)이라 한다. 성공확률이 p인 베르누이 시행을 n번 독립적으로 반복 시행할 때, '성공횟수(=X)'가 x일 확률은 다음과 같이 표시할 수 있다. $$ P(X=x) = (\frac{n}{x})p^{x}(1-p)^{n-x}, x=0,1,2, ..., n $$ 이항분포의 평균은 E(X)=np, 분산은 Var(X)=np(1-p) 이다. 증명은  https://proofwiki.org/wiki/Variance_of_Binomial_Distribution  참고하면 된다. 여기에서 n , p 를 이항분포의 모수(parameter)라 한다. 만약 n=1이라면, 이항분포 B ( n , p )는 '1(성공)'의 확률이 p 인 베르누이분포이다. 참고로 모수는 모집단의 특성값으로, 평균, 분산, 성공확률 등을 예시로 들 수 있다.
댓글 쓰기
자세한 내용 보기

Odds Ratio and Relative Risk ; 오즈비와 상대위험도

  Odds Ratio 는 임상에서 매우 많이 사용되는 개념이다. 그러나 'Odds' 라는 개념이 직관적으로 잘 와닿지 않기 때문에 흔히 오용되기도 하는 개념이라 가장 먼저 잡고가야 할 주제로 삼았다.   오즈비는 범주형 자료에서 사용되는데, 오즈비를 보면서 가장 많이 접하게 될  2X2 분할표는 다음과 같이 생겼다.   Event Normal Total Exposed A B A + B Non-exposed C D C + D 흔히 하는 실수가 오즈비(Odds Ratio)를 해석할 때, 상대위험도(Relative risk)를 해석하듯이 한다는 점이다. 따라서 오즈비와 상대위험도의 각 개념에 대해서 살펴보고 넘어가도록 하자.   ❗Odds Ratio와 Relative Risk의 공통점 : 상대적인 비율 을 나타낸다. Public health / Medical 에서 Odds Ratio or Relative Risk를 사용하는 이유 - 어떤 조건에서 더 위험한지를 수치적으로 나타내기 위해서 사용 한다. 예를 들면, "흡연(조건)"을 하는 사람은 비흡연자에 비해 "폐암(Event)" 발생에 있어서 몇 배가 더 위험한가? 와 같은 질문에 대한 해답으로 많이 사용된다.   ✅위와 같은 2X2 이차원 분할표에서 Odds Ratio (오즈비) 의 수식적 정의 는 다음과 같다. P1 = A/(A+B) ; P2 = C/(C+D) Odds1 = P1/(1-P1) ; Odds2 = P2/(1-P2) Odds Ratio = Odds1/Odds2 = A*D/B*C ✅ 한편 2X2 분할표에서 Relative Risk (상대위험도) 의 수식적 정의 는 ...
댓글 쓰기
자세한 내용 보기

Odds Ratio and Relative Risk ; 오즈비와 상대위험도 part. 2

 지난 글에서 2X2 분할표에서 많이 사용되는 오즈비와 상대위험도의 개념에 대해서 살펴보았다. 그 중에서도 지난 글에서는 오즈비를 사용할 수밖에 없는 경우에 대해 살펴보았다.  상대위험도가 직관적으로 이해하기 쉽고 위험비에 대한 쉬운 해석을 가능하게 하지만, 그럼에도 불구하고 보건 or 의학 계열에서 오즈비를 많이 사용 할 수밖에 없는 이유에 대해 살펴보았다. 또한 오즈비와 상대위험도는 가끔 동일하게 해석되기도 한다. (자세한 내용은 이전 글로..) 그럼 이번 글에서는 오즈비와 상대위험도를 동일하게 해석할 수 있는 경우 에 대해 살펴보도록 하겠다. 먼저 다음과 같은 오즈비의 특성을 이해해야 한다. 오즈비의 중요 특성: 상대적인 위험도를 과장하는 측면 이 있다. 이는 굉장히 중요한 오즈비의 특성인데, Relative Risk 값보다 항상 큰 값을 가진다. 그리고 이는 해당 Event가 흔하게 일어날 수록 더욱 더 과장 된다. 📋예를 들어 보자. 따듯한 차를 마셨을 때와 방안 온도의 차를 마셨을 때 체온이 상승하는지 아니면 그대로 유지되는지에 대해 조사하고 다음과 같은 분할표를 얻었다.   체온 상승 유지 Total Warm tea 90 10 100 Normal temp 20 180 200 먼저 Relative Risk 상대위험도 를 구해보자. $$ \frac{90/100}{20/200} = 9 $$ 이번엔 Odds Ratio 오즈비 를 구해보자. (유도과정은 이전 글 참고) $$ \frac{90 * 180}{20 * 10} = 81 $$ 이번엔 방금 구한 상대위험도와 오즈비를 해석해보자. 📉 RR : 상대위험도는 9로, 이는 따듯한 차를 마신다면 체온이 상승할 확률이 방안 온도의 차를 마셨을 때보다 체온이 상승할 확률...
댓글 쓰기
자세한 내용 보기