Radiomics: Feature selection 3

 Demircioğlu, Aydin PhD Benchmarking Feature Selection Methods in Radiomics, Investigative Radiology: January 18, 2022 - Volume - Issue - doi: 10.1097/RLI.0000000000000855

High dimensionality of the datasets and small sample sizes are critical problems in radiomics.

Therefore, removing redundant features and irrelevant features is needed.

Overall, per dataset, 

30 different feature selection methods +

10 classifiers +

70 hyperparameter settings

After each feature selection method, 1, 2, ..., 64 features were selected.

Altogether, 14,700=30✕70✕7 models were fitted, each with a 10-fold cross-validation.

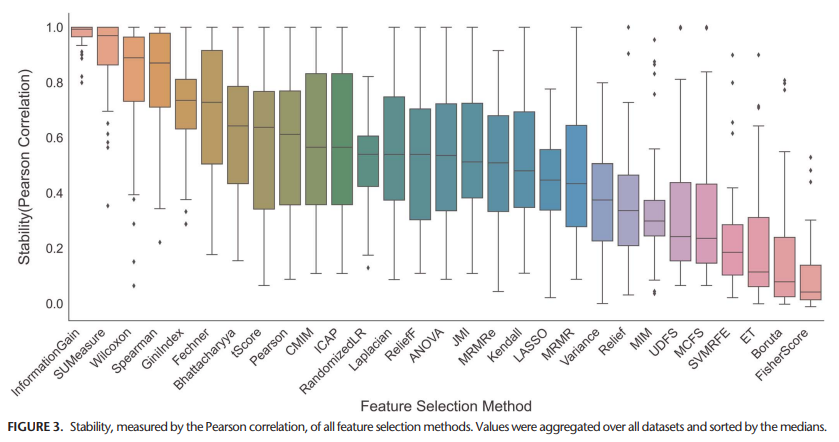
More complex methods are more unstable than simpler feature selection methods.

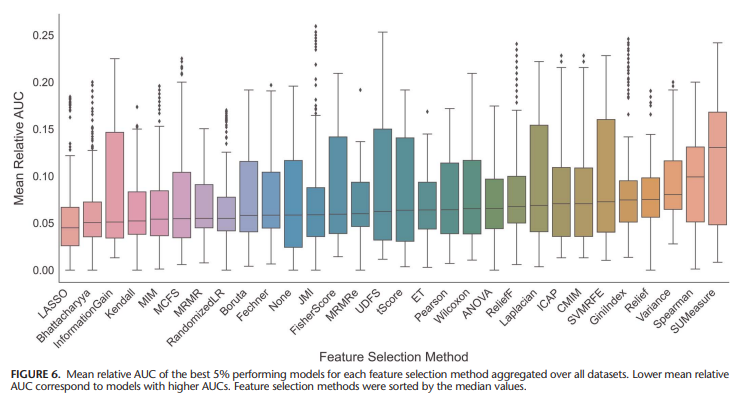
LASSO performed best when analysing the predictive performance, though it showed only average feature stability.

Longer training times and higher computational complexity of the feature selection method do not mean for high predictive performance necessarily.

Obtaining a more stable model might entail a slight loss in predictive performance.

Therefore, this paper recommends considering feature selection methods that are not too complex.

 ⇨ ①ANOVA, ②LASSO, and ③MRMRe are good candidates for feature selection.

 ⇨ if these 3 methods do not show adequate predictive performance, another methods like Boruta or MIM(mutual information) should be considered.

 ⇨ or fast methods like Pearson, multicluster feature selection, unsupervised discriminative feature selection could be considered.

No single feature selection method dominated others.

The features generated by a pretrained convolutional neural network are more robust, show smaller variance, and are less affected by acquisition parameters.