Why using a paired t test to assess agreement is problematic? by Nikolaos Pandis
https://doi.org/10.1016/j.ajodo.2021.07.001
Agreement를 평가함에 있어 paired t-test를 사용하는 논문들이 몇 있다.
임상논문에서 의료기기가 측정한 것의 일치성, 혹은 의료행위자 A와 B가 측정한 것이 비슷한지를 측정하는 일들이 꽤 많은데, 여전히 많은 논문들에서 paired t-test에서 p>0.05 라는 통계 결과를 얻었을 때 '두 기기에서 측정한 수치는 일치한다.' 혹은 '의사A와 의사B가 측정한 수치는 일치한다.' 라는 결과를 내린다.
통계를 배울 때, "짝지어진 두 모집단의 차이를 보고 싶을 때는 paired t-test를 사용한다." 라고 많이들 배우는데, 아마 이렇게 배우기(?) 때문에 '그럼 paired t-test의 p-value가 0.05보다 크면 두 집단 간 차이가 없다는 것이겠네?'라고 많은 사람들의 생각이 이어지는듯하다.
그러나 내가 통계적으로 살펴보고 싶은 것이 "Agreement"라면 paired t-test를 사용하는 것은 잘못 되었다.
그 이유에 대해서는 다음 두 개의 시나리오를 이용해 설명해보도록 하겠다.
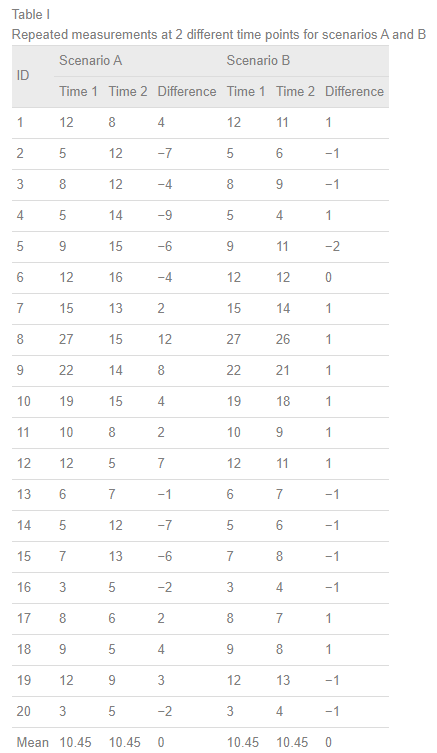
시나리오A와 시나리오B에는 시간 차이를 두고 같은 subject를 측정한 Time1 수치와 Time2 수치가 있다. 시나리오A와 시나리오B 모두 Time1과 Time2에서 측정된 수치의 평균은 10.45로 동일하다.
✔️먼저 시나리오A를 살펴보자.
시나리오A에서 Time1과 Time2의 평균은 10.45로 동일하므로, 차이 d의 평균도 0이고 따라서 paired t-test를 진행하면 p-value가 1로 나올 것이다.
그럼 Time1과 Time2가 동일한 수치를 냈다고 결론지을 수 있는가?
시나리오A의 각 subject를 대상으로 시간 차이를 두고 측정한 Time1과 Time2는 [-9 ~ 12] 까지 꽤 큰 차이가 있다.
✔️이번에는 시나리오B를 살펴보자.
여기에서도 마찬가지로 Time1과 Time2의 평균은 10.45로 동일하며, 차이 d의 평균 역시 0이다. 그렇기에 시나리오B의 데이터로 paired t-test를 진행하면 p-value 1을 얻을 것이다. 시나리오A와 다른 점은 각 subject에서 Time1과 Time2의 차이가 [-2 ~ 1]로 훨씬 작다는 점이다.
paired t-test 결과, 시나리오B는 시나리오A와 같이 p-value가 1이므로 두 경우 모두 "불일치의 증거가 없다. -> 두 측정치는 일치한다."라고 결론 내릴 수 있을까?
Paired t-test의 귀무가설은 "두 그룹의 모평균의 차이는 없다." 이므로, 시나리오A에서 p-value가 1이기 때문에 귀무가설을 기각할 수 없고, 따라서 불일치의 증거가 없다는 잘못된 해석이다.
❌두 측정 간의 agreement를 통계적으로 측정하고자 할 때, paired t-test를 사용한다는 것부터 잘못되었다. 직관적으로도 시나리오A와 시나리오B에서 같은 결과를 내는 것은 잘못 되었다고 보인다.
✔️그럼 왜 이런 문제가 발생할까?
이러한 문제는 각각의 observation을 살펴보는 것이 아니고 "평균"을 살펴보기 때문에 발생한다. 예를 들어, 임상시험처럼 '투여군'과 '대조군' 간, 정말 전반적인 "그룹" 간의 차이가 중요할 때에는 paired t-test를 사용할 수 있다. 그러나 각 observation의 차이가 중요한 Agreement를 살펴보고자 할 때 paired t-test를 사용하면 위의 예시처럼 평균의 함정에 빠질 수 있다.
댓글
댓글 쓰기