Processing math: 25%
  통계 기초 : 표준오차 vs 표준편차 (standard error & standard deviation) 기본 콘텐츠로 건너뛰기

통계 기초 : 표준오차 vs 표준편차 (standard error & standard deviation)

 통계를 살펴보면서 헷갈리는 것을 꼽으면 표준오차와 표준편차의 차이점을 들 수 있다.


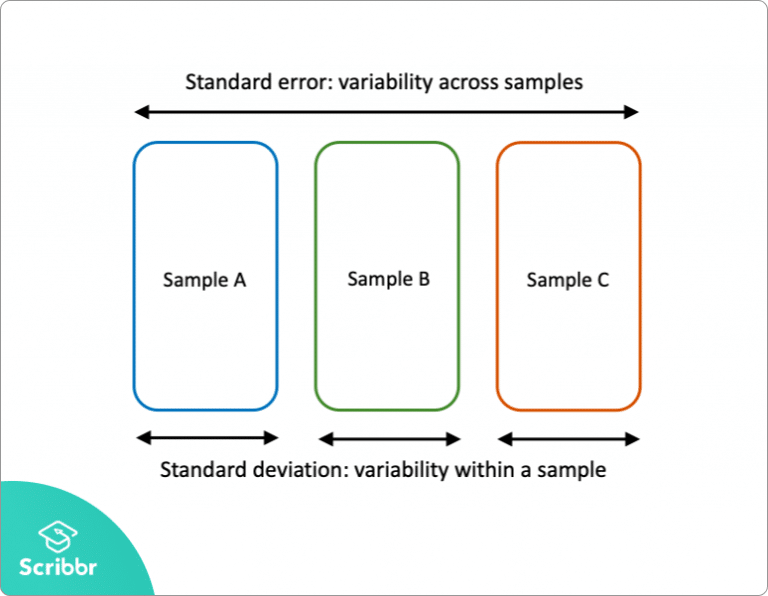
표준편차와 표준오차에 대해 명확하게 나타낸 그림이 있어 가져왔다. 

(출처는 그림 안에 있음)


표준편차와 표준오차는 한국어로 표현했을 때, 단 한 글자의 차이밖에 없기 때문에 나만 그럴 수 있겠지만.. 더 헷갈린다.


먼저 표준편차에 대해서 살펴보자.

예를 들어, 전국의 성인 남녀의 몸무게를 조사하기 위해 1,000명을 랜덤으로 추출하고자 한다. 

여기에서 모집단은 전국의 성인 남녀이고, 표본은 랜덤으로 추출된 1,000명의 성인 남녀이다.

그럼 표본의 크기가 1,000인 성인 남녀의 몸무게의 평균을 62kg, 표준편차는 4.5kg라 하자.


𝓧¡ 를 표본조사를 통해 얻은 각 관측치라고 할 때, 표준편차의 제곱을 구하는 식은 다음과 같다.

 S^2=\frac{\sum_{i=1}^{n}(x_i-\overline{x})^2}{n-1}

위 수식을 통해 표준편차란, 표본 조사로 얻은 각 관측값과 표본평균의 차이를 나타낸다고 할 수 있다. 

모집단의 표준편차를 구할 때에는 분모에 n-1 대신 n으로 나누면 된다.



이번에는 표준오차를 살펴볼 차례이다.

바로 표준오차의 수식을 살펴보자.

 SE=s/\sqrt{n}

표준오차는 표준편차를 표본크기의 제곱근으로 나눈 값이다. 따라서 표본의 크기(n)가 커질수록 표준오차의 값은 작아진다.


그럼 표준오차는 무엇을 의미할까? 표준오차는 "표본평균들의 편차"를 의미한다. 

원래 샘플링 오류를 줄이기 위해서 모집단에서 여러 번 표본추출을 하여 여러 표본 그룹이 있어야 하지만 현실적인 이유로 이는 불가능한 경우가 대다수다.

대부분의 경우는 모집단에서 한 번의 표본추출을 하고, 이 표본들이 모집단을 대표한다고 추정한다. 따라서 위의 예시와 같이 표본 1,000명이라는 표본의 크기 n과, 이 표본의 표준편차인 4.5kg를 이용하여 표준오차를 구하게 된다. 

따라서 위 예시에서 표준오차는 4.5/√1000 ≒ 1.423이다.


표본의 수가 충분히 크면 중심극한정리에 의해 표준평균은 정규분포를 따르므로, 이를 통해 95% 신뢰구간을 구하자면, [62 ± (1.96*1.423)]가 된다.



태그

라벨:

댓글

댓글 쓰기

이 블로그의 인기 게시물

통계 : Dummy Variable Trap

 Regression model을 만들다 보면, 독립변수로 명목형 변수를 사용할 때가 많다. 지역이나 성별, biomaker유/무 등이 대표적으로 많이 사용되는 명목형 변수로, 특히 medical 저널에서는 성별을 covariate으로 취급하여 성별에 따른 종속변수의 차이를 보고자 할 때가 많다. 명목형 변수들은 Dummy Variable로 바꾸어서 regression model을 만드는데, one hot 인코딩 방식으로 더미 변수들을 만든다. 예를 들면,  ❕ male=0, female=1 ❕ Biomarker유=1, Biomarker무=0 이런식으로 만든다. 이와 같은 binary 데이터들은 더미 변수로 만드는 것도 쉽고 큰 문제가 되지 않는다. one-hot encoding의 이유는, 0과 1 대신 빨간색, 녹색, 파란색을 1,2,3 으로 코딩해버리면, 적합한 모델은 숫자가 더 큰 3을 빨간색보다 더 중요한 인자로 생각하게 되기 때문이다. 학력처럼 순서형이면 각 숫자에 의미가 있지만 여러 컬러처럼 단순 명목형일 때에는 one-hot 인코딩을 해야한다.  (단, 컬러가 연함 - 진함과 같이 순서형이라면 굳이 one-hot 인코딩을 안해도 된다.) one-hot encoding 의 예시는 아래 세 가지 카테고리로 보면 더 명확하게 이해가 된다. (image출처: https://towardsdatascience.com/encoding-categorical-variables-one-hot-vs-dummy-encoding-6d5b9c46e2db) 그럼 binary 말고 여러 카테고리가 있는 변수의 경우는 어떤 식으로 더미 변수를 만들까? Regression 모델을 만들 때에는 k개의 카테고리가 있다면, k-1개의 더미변수를 생성하게 된다. 위 그림에서 Blue일 때, d1, d2, d3 모두 0으로 코딩해도 Red, Green과 차이가 있으므로, d1과 d2만 만들어도 무방하다는 의미이다. 즉, d1과 d2가 0일 때, Blue가...
댓글 쓰기
자세한 내용 보기

통계 기초 : 확률 분포 - (1) 이항분포

Binomial distribution 이항분포에 앞서 베르누이분포가 있다. 모든 가능한 결과가 두 가지인 실험(표본공간이 {불량품, 양호품},{찬성, 반대} 등)을 베르누이 시행(Bernoulli trial)이라 한다. 성공확률을 p 라고 할 때, '성공'이면 1, '실패'면 0으로 대응시키는 확률변수를 베르누이 확률변수라 한다. 베르누이 확률변수 X의 확률분포는 다음과 같이 정의할 수 있다. P(X=x) = p^{x}(1-p)^{1-x}, x=0,1 따라서, X=0인 경우에는 P(X=0) = (1-p)이고, X=1인 경우에는 P(X=1) = p가 된다. 베르누이분포의 평균은 E(X)=p, Var(X)=p(1-p) 이다. 이처럼 동일한 성공확률을 가진 베르누이 시행 을 독립적 으로 반복 하여 시행할 때, 'X=성공횟수'의 분포를 이항분포(binomial distribution)이라 한다. 성공확률이 p인 베르누이 시행을 n번 독립적으로 반복 시행할 때, '성공횟수(=X)'가 x일 확률은 다음과 같이 표시할 수 있다. P(X=x) = (\frac{n}{x})p^{x}(1-p)^{n-x}, x=0,1,2, ..., n 이항분포의 평균은 E(X)=np, 분산은 Var(X)=np(1-p) 이다. 증명은  https://proofwiki.org/wiki/Variance_of_Binomial_Distribution  참고하면 된다. 여기에서 n , p 를 이항분포의 모수(parameter)라 한다. 만약 n=1이라면, 이항분포 B ( n , p )는 '1(성공)'의 확률이 p 인 베르누이분포이다. 참고로 모수는 모집단의 특성값으로, 평균, 분산, 성공확률 등을 예시로 들 수 있다.
댓글 쓰기
자세한 내용 보기

Odds Ratio and Relative Risk ; 오즈비와 상대위험도

  Odds Ratio 는 임상에서 매우 많이 사용되는 개념이다. 그러나 'Odds' 라는 개념이 직관적으로 잘 와닿지 않기 때문에 흔히 오용되기도 하는 개념이라 가장 먼저 잡고가야 할 주제로 삼았다.   오즈비는 범주형 자료에서 사용되는데, 오즈비를 보면서 가장 많이 접하게 될  2X2 분할표는 다음과 같이 생겼다.   Event Normal Total Exposed A B A + B Non-exposed C D C + D 흔히 하는 실수가 오즈비(Odds Ratio)를 해석할 때, 상대위험도(Relative risk)를 해석하듯이 한다는 점이다. 따라서 오즈비와 상대위험도의 각 개념에 대해서 살펴보고 넘어가도록 하자.   ❗Odds Ratio와 Relative Risk의 공통점 : 상대적인 비율 을 나타낸다. Public health / Medical 에서 Odds Ratio or Relative Risk를 사용하는 이유 - 어떤 조건에서 더 위험한지를 수치적으로 나타내기 위해서 사용 한다. 예를 들면, "흡연(조건)"을 하는 사람은 비흡연자에 비해 "폐암(Event)" 발생에 있어서 몇 배가 더 위험한가? 와 같은 질문에 대한 해답으로 많이 사용된다.   ✅위와 같은 2X2 이차원 분할표에서 Odds Ratio (오즈비) 의 수식적 정의 는 다음과 같다. P1 = A/(A+B) ; P2 = C/(C+D) Odds1 = P1/(1-P1) ; Odds2 = P2/(1-P2) Odds Ratio = Odds1/Odds2 = A*D/B*C ✅ 한편 2X2 분할표에서 Relative Risk (상대위험도) 의 수식적 정의 는 ...
댓글 쓰기
자세한 내용 보기